常见数据结构总结

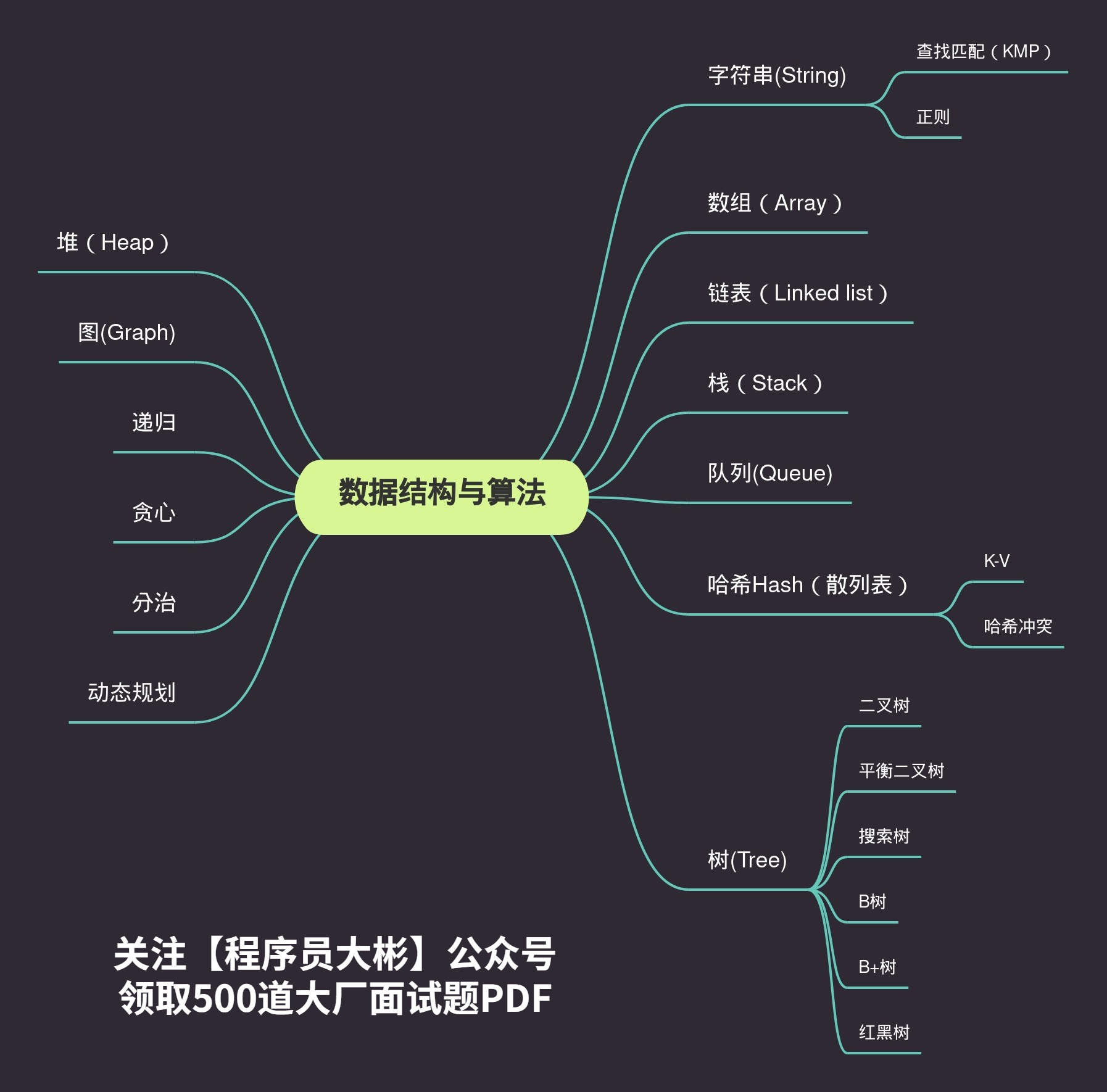
arcstack2023年6月20日计算机基础数据结构约 3228 字大约 11 分钟

各种数据结构应用场景

数组

数组的优点:

数组的缺点:

链表

优点：

缺点：存取速度很慢

分类

哈希表

散列表（Hash table，也叫哈希表），是根据关键码值(Key value)而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

栈

我们把类似于弹夹那种先进后出的数据结构称为栈，栈是限定仅在表尾进行插入和删除操作的线性表，我们把允许插入和删除的一端称为栈顶，另一端称为栈底，不含任何数据元素的栈称为空栈，栈又称后进后出的线性表，简称LIFO结构。

栈的特殊之处在于限制了这个线性表的插入和删除位置，它始终只在栈顶进行。这也就使得：栈底是固定的，最先进栈的只能在栈底。

栈的插入操作，叫做进栈；栈的删除操作叫做出栈。

队列

队列是只允许在一端进行插入操作，而在另一端进行删除操作的线性表，队列是一种先进先出的线性表，简称FIFO，允许插入的一端称为队尾（Rear），允许删除的一端称为队头(Front)。向队中插入元素称为进队，新元素进队后成为新的队尾元素；向队中删除元素称为出队，元素出队后，其后继元素就成为新的队头元素。

树

树是一种数据结构，它看上去像一棵 "圣诞树"，它的根在上，叶朝下。

树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。

二叉树

最多有两棵子树的树被称为二叉树

满二叉树: 二叉树中所有非叶子结点的度都是2，且叶子结点都在同一层次上

完全二叉树: 如果一个二叉树与满二叉树前m个节点的结构相同，这样的二叉树被称为完全二叉树

二叉查找树

指一棵空树或者具有下列性质的二叉树。

AVL树

平衡二叉搜索树，它是一 棵空树或它的左右两个子树的高度差的绝对值不超过1。

简单了解一下左旋与右旋的概念。

左旋与右旋就是为了解决不平衡问题而产生的，我们构建一颗AVL树的过程会出现结点平衡因子（平衡因子就是二叉排序树中每个结点的左子树和右子树的高度差。）绝对值大于1的情况，这时就可以通过左旋或者右旋操作来达到平衡的目的。

四种旋转情况

红黑树

红黑树是对AVL树的优化，只要求部分平衡，用非严格的平衡来换取增删节点时候旋转次数的降低，提高了插入和删除的性能。查找性能并没有提高，查找的时间复杂度是O(logn)。红黑树通过左旋、右旋和变色维持平衡。

对于插入节点，AVL和红黑树都是最多两次旋转来实现平衡。对于删除节点，avl需要维护从被删除节点到根节点root这条路径上所有节点的平衡，旋转的量级为O(logN)，而红黑树最多只需旋转3次。

红黑树的特性：

优点：相比avl树，红黑树插入删除的效率更高。红黑树维持红黑性质所做的红黑变换和旋转的开销，相较于avl树维持平衡的开销要小得多。

应用场景

B树

也称B-树，属于多叉树又名平衡多路查找树。

规则：

B-树的特性：

  1. 关键字集合分布在整颗树中；
  2. 任何一个关键字只出现在一个节点中；
  3. 搜索有可能在非叶子结点结束；

B+树是B-树的变体，也是一种多路搜索树。B+的搜索与B-树基本相同，区别是B+树只有达到叶子结点才命中，B-树可以在非叶子结点命中。B+树更适合文件索引系统。

B-和B+树的区别：

图

图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为: G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

和线性表，树的差异:

相关术语

顶点Vi的度(Degree)是指在图中与Vi相关联的边的条数。对于有向图来说，有入度(In-degree)和出度(Out-degree)之分，有向图顶点的度等于该顶点的入度和出度之和。

若无向图中的两个顶点V1和V2存在一条边(V1,V2)，则称顶点V1和V2邻接(Adjacent)；

若有向图中存在一条边<V3,V2>，则称顶点V3与顶点V2邻接，且是V3邻接到V2或V2邻接直V3；

在无向图中，若从顶点Vi出发有一组边可到达顶点Vj，则称顶点Vi到顶点Vj的顶点序列为从顶点Vi到顶点Vj的路径(Path)。

若从Vi到Vj有路径可通，则称顶点Vi和顶点Vj是连通(Connected)的。

有些图的边或弧具有与它相关的数字，这种与图的边或弧相关的数叫做权(Weight)。

类型

无向图

如果图中任意两个顶点之间的边都是无向边(简而言之就是没有方向的边)，则称该图为无向图(Undirected graphs)。

无向图中的边使用小括号“()”表示; 比如 (V1,V2);

有向图

如果图中任意两个顶点之间的边都是有向边(简而言之就是有方向的边)，则称该图为有向图(Directed graphs)。

有向图中的边使用尖括号“<>”表示; 比如/<V1,V2>

完全图

图的存储结构

1、邻接矩阵

图的邻接矩阵(Adjacency Matrix)存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。

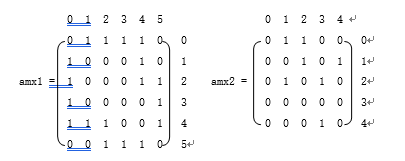
2、邻接表

邻接表由表头节点和表节点两部分组成，图中每个顶点均对应一个存储在数组中的表头节点。如果这个表头节点所对应的顶点存在邻接节点，则把邻接节点依次存放于表头节点所指向的单向链表中。

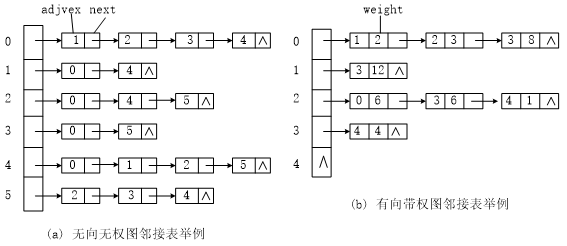
下面给出建立图的邻接表中所使用的边结点类的定义

public class EdgeNode {     //定义邻接表中的边结点类型
    int adjvex;             //邻接点域
    int weight;             //边的权值域，假定为整型，对于无权图，边的权值为1
    EdgeNode next;          //指向下一个边结点的链接域
    public EdgeNode(int adj, EdgeNode nt) 
    {     //对无权图中的边结点进行初始化
        adjvex=adj; next=nt; weight=1;
    }
    public EdgeNode(int adj, int wgt, EdgeNode nt) 
    {     //对有权图中的边结点进行初始化
        adjvex=adj; next=nt; weight=wgt;
    }
}

图的接口类定义如下：

public interface Graph
     {
         boolean createGraph(EdgeElement[]d);  //根据边集数组参数d建立一个图
         int graphType();                   //返回图的类型
         int vertices();                    //返回图中的顶点数
         int edges();                       //返回图中的边数
         boolean find(int i, int j);        //从图中查找一条边(i,j)是否存在
         boolean putEdge(EdgeElement theEdge); //向图中插入一条边theEdge
         boolean removeEdge(int i, int j);     //从图中删除一条边(i,j)
         int degree(int i);                 //返回顶点i的度
         int inDegree(int i);               //返回顶点i的入度
         int outDegree(int i);              //返回顶点i的出度
         void output();                     //以图的顶点集和边集的形式输出一个图
         void depthFirstSearch(int v);      //从顶点v开始深度优先搜索遍历图
         void breadthFirstSearch(int v);    //从顶点v开始广度优先搜索遍历图
         void clearGraph();                 //清除图中的所有内容
     }

图的遍历

深度优先遍历

private void dfs(int i, boolean[] visited) {
    System.out.printl(i + " ");
    visited[i] = true;
    EdgeNode p = a[i];
    while(p != null) {
        int j = p.adjvex;
        if(!visited[j]) {
            dfs(j, visited);
        }
        p = p.next;
    }
}

广度优先搜索

private void bfs(int i, boolean[] visited) {
    LinkedList<Integer> queue = new LinkedList<>();
    System.out.print(i + " ");
    visited[i] = true;
    queue.offer(i);
    while(!queue.isEmpty()) {
        int k = queue.poll();
        EdgeNode p = a[k];

        while(p != null) {
            int j = p.adjvex;
            if(!visited[j]) {
                System.out.print(j + " ");
                visited[j] = true;
                queue.offer(j);
            }
            p = p.next;
        }
    }
}