62. 不同路径
62. 不同路径
题目描述
一个机器人位于一个 m x n 网格的左上角 。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角。
问总共有多少条不同的路径?
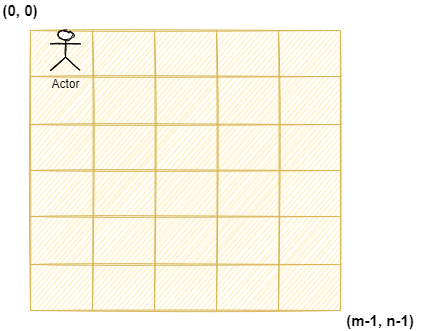
示例:
输入:m = 3, n = 7
输出:28
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
解题思路
首先了解下动态规划的思想。
动态规划用于处理有重叠子问题的问题。其基本思想:假如要解一个问题,需要先将问题分解成子问题,求出子问题的解,再根据子问题的解得出原问题的解。
动态规划算法会将计算出来的子问题的解存储起来,以便下次遇到同一个子问题的时候直接可以得到该子问题的解,减少重复计算。
动态规划的解题思路:1、状态定义;2、状态转移方程;3、初始状态;4、确定遍历顺序。
接下来分步骤讲解本题目的思路。
1、首先是状态定义。假设 dp[i][j] 是到达 (i, j) 的路径数量,dp[2][2]就是到达(2, 2)的路径数量。
2、然后是状态转移方程。根据题意,只能向右和向下运动,当前位置(i, j)只能从(i-1, j)和(i, j-1)两个方向走过来,由此可以确定状态方程为dp[i][j] = dp[i-1][j] + dp[i][j-1]。
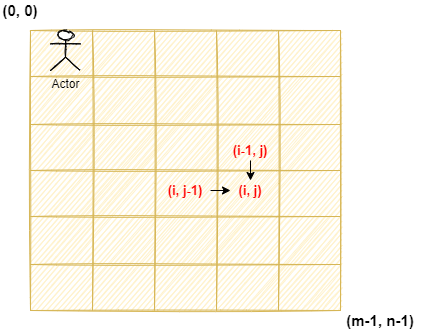
3、初始状态。对于第一行 dp[0][j]和第一列 dp[i][0],由于都在边界,只有一个方向可以走,所以只能为 1。
4、确定遍历顺序。dp[i][j]是从其上边和左边推导而来,所以按照从左到右,从上到下的顺序来遍历。
代码实现
使用二维数组dp[][]保存中间状态,时间复杂度和空间复杂度都是O(m*n)。
public int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
//初始化
for (int i = 0; i < n; i++) {
dp[0][i] = 1;
}
//初始化
for (int i = 0; i < m; i++) {
dp[i][0] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
//状态方程
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
优化1:根据状态转移方程dp[i][j] = dp[i-1][j] + dp[i][j-1]可知,只需要保存当前行与上一行的数据即可,空间复杂度可以优化为O(2n),具体代码如下:
public int uniquePaths(int m, int n) {
int[] preRow = new int[n];
int[] curRow = new int[n];
//初始化
for (int i = 0; i < n; i++) {
preRow[i] = 1;
curRow[i] = 1;
}
for (int i = 1; i < m; i++){
for (int j = 1; j < n; j++){
curRow[j] = curRow[j-1] + preRow[j];
}
preRow = curRow.clone();
}
return curRow[n-1];
}
优化2:上述代码还可以继续优化,对于curRow[j] = curRow[j-1] + preRow[j],在未赋值之前curRow[j]就是当前行第i行的上一行第j列的值(这里可能不太好理解,小伙伴们好好思考一下),也就是说未赋值之前curRow[j]与preRow[j]相等,因此curRow[j] = curRow[j-1] + preRow[j]可以写成curRow[j] += curRow[j-1],优化1代码中的preRow数组可以不用,只需要curRow数组即可,代码如下:
public int uniquePaths(int m, int n) {
int[] curRow = new int[n];
//初始化
for (int i = 0; i < n; i++) {
curRow[i] = 1;
}
for (int i = 1; i < m; i++){
for (int j = 1; j < n; j++){
curRow[j] += curRow[j-1];
}
}
return curRow[n-1];
}
这道腾讯面试题,算是动态规划里面比较简单的题目,虽然不难,但是在面试时氛围比较紧张的情况下,想要一次性bug free做出来,并且做到最优解,还是有点难度的。