树 - 平衡二叉树(AVL)
树 - 平衡二叉树(AVL)
平衡二叉树(Balanced Binary Tree)具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等。 最小二叉平衡树的节点的公式如下 F(n)=F(n-1)+F(n-2)+1 这个类似于一个递归的数列,可以参考Fibonacci数列,1是根节点,F(n-1)是左子树的节点数量,F(n-2)是右子树的节点数量。@pdai
什么是AVL树
AVL树是高度平衡的二叉树。它的特点是: AVL树中任何节点的两个子树的高度最大差别为1。

上面的两张图片,左边的是AVL树,它的任何节点的两个子树的高度差别都<=1;而右边的不是AVL树,因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3,而以8为根节点的树的高度是1)。
动画效果请参考 AVL Tree 在新窗口打开

AVL树的实现
节点
节点定义
AVLTree是AVL树对应的类,而AVLTreeNode是AVL树节点,它是AVLTree的内部类。AVLTree包含了AVL树的根节点,AVL树的基本操作也定义在AVL树中。AVLTreeNode包括的几个组成对象:
- key -- 是关键字,是用来对AVL树的节点进行排序的。
- left -- 是左孩子。
- right -- 是右孩子。
- height -- 是高度。
public class AVLTree<T extends Comparable<T>> {
private AVLTreeNode<T> mRoot; // 根结点
// AVL树的节点(内部类)
class AVLTreeNode<T extends Comparable<T>> {
T key; // 关键字(键值)
int height; // 高度
AVLTreeNode<T> left; // 左孩子
AVLTreeNode<T> right; // 右孩子
public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) {
this.key = key;
this.left = left;
this.right = right;
this.height = 0;
}
}
......
}
树的高度
关于高度,有的地方将"空二叉树的高度是-1",而本文采用维基百科上的定义: 树的高度为最大层次。即空的二叉树的高度是0,非空树的高度等于它的最大层次(根的层次为1,根的子节点为第2层,依次类推)。
/* * 获取树的高度 */
private int height(AVLTreeNode<T> tree) {
if (tree != null)
return tree.height;
return 0;
}
public int height() {
return height(mRoot);
}
比较大小
/* * 比较两个值的大小 */
private int max(int a, int b) {
return a>b ? a : b;
}
旋转
如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态: LL(左左),LR(左右),RR(右右)和RL(右左)。下面给出它们的示意图:

上图中的4棵树都是"失去平衡的AVL树",从左往右的情况依次是: LL、LR、RL、RR。除了上面的情况之外,还有其它的失去平衡的AVL树,如下图:

上面的两张图都是为了便于理解,而列举的关于"失去平衡的AVL树"的例子。总的来说,AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一,它们都由各自的定义:
(1) LL: LeftLeft,也称为"左左"。插入或删除一个节点后,根节点的左子树的左子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。 例如,在上面LL情况中,由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(2) LR: LeftRight,也称为"左右"。插入或删除一个节点后,根节点的左子树的右子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。 例如,在上面LR情况中,由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(3) RL: RightLeft,称为"右左"。插入或删除一个节点后,根节点的右子树的左子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。 例如,在上面RL情况中,由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
(4) RR: RightRight,称为"右右"。插入或删除一个节点后,根节点的右子树的右子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。 例如,在上面RR情况中,由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。AVL失去平衡之后,可以通过旋转使其恢复平衡,下面分别介绍"LL(左左),LR(左右),RR(右右)和RL(右左)"这4种情况对应的旋转方法。
LL的旋转
LL失去平衡的情况,可以通过一次旋转让AVL树恢复平衡。如下图:

图中左边是旋转之前的树,右边是旋转之后的树。从中可以发现,旋转之后的树又变成了AVL树,而且该旋转只需要一次即可完成。 对于LL旋转,你可以这样理解为: LL旋转是围绕"失去平衡的AVL根节点"进行的,也就是节点k2;而且由于是LL情况,即左左情况,就用手抓着"左孩子,即k1"使劲摇。将k1变成根节点,k2变成k1的右子树,"k1的右子树"变成"k2的左子树"。
/* * LL: 左左对应的情况(左单旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) {
AVLTreeNode<T> k1;
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = max( height(k2.left), height(k2.right)) + 1;
k1.height = max( height(k1.left), k2.height) + 1;
return k1;
}
RR的旋转
理解了LL之后,RR就相当容易理解了。RR是与LL对称的情况!RR恢复平衡的旋转方法如下:

图中左边是旋转之前的树,右边是旋转之后的树。RR旋转也只需要一次即可完成。
/* * RR: 右右对应的情况(右单旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) {
AVLTreeNode<T> k2;
k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = max( height(k1.left), height(k1.right)) + 1;
k2.height = max( height(k2.right), k1.height) + 1;
return k2;
}
LR的旋转
LR失去平衡的情况,需要经过两次旋转才能让AVL树恢复平衡。如下图:

第一次旋转是围绕"k1"进行的"RR旋转",第二次是围绕"k3"进行的"LL旋转"。
/* * LR: 左右对应的情况(左双旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) {
k3.left = rightRightRotation(k3.left);
return leftLeftRotation(k3);
}
RL的旋转
RL是与LR的对称情况!RL恢复平衡的旋转方法如下:

第一次旋转是围绕"k3"进行的"LL旋转",第二次是围绕"k1"进行的"RR旋转"。
/* * RL: 右左对应的情况(右双旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
插入
插入节点的代码
/* * 将结点插入到AVL树中,并返回根节点 * * 参数说明: * tree AVL树的根结点 * key 插入的结点的键值 * 返回值: * 根节点 */
private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) {
if (tree == null) {
// 新建节点
tree = new AVLTreeNode<T>(key, null, null);
if (tree==null) {
System.out.println("ERROR: create avltree node failed!");
return null;
}
} else {
int cmp = key.compareTo(tree.key);
if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况
tree.left = insert(tree.left, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) == 2) {
if (key.compareTo(tree.left.key) < 0)
tree = leftLeftRotation(tree);
else
tree = leftRightRotation(tree);
}
} else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况
tree.right = insert(tree.right, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.right) - height(tree.left) == 2) {
if (key.compareTo(tree.right.key) > 0)
tree = rightRightRotation(tree);
else
tree = rightLeftRotation(tree);
}
} else { // cmp==0
System.out.println("添加失败: 不允许添加相同的节点!");
}
}
tree.height = max( height(tree.left), height(tree.right)) + 1;
return tree;
}
public void insert(T key) {
mRoot = insert(mRoot, key);
}
删除
删除节点的代码
/* * 删除结点(z),返回根节点 * * 参数说明: * tree AVL树的根结点 * z 待删除的结点 * 返回值: * 根节点 */
private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) {
// 根为空 或者 没有要删除的节点,直接返回null。
if (tree==null || z==null)
return null;
int cmp = z.key.compareTo(tree.key);
if (cmp < 0) { // 待删除的节点在"tree的左子树"中
tree.left = remove(tree.left, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.right) - height(tree.left) == 2) {
AVLTreeNode<T> r = tree.right;
if (height(r.left) > height(r.right))
tree = rightLeftRotation(tree);
else
tree = rightRightRotation(tree);
}
} else if (cmp > 0) { // 待删除的节点在"tree的右子树"中
tree.right = remove(tree.right, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) == 2) {
AVLTreeNode<T> l = tree.left;
if (height(l.right) > height(l.left))
tree = leftRightRotation(tree);
else
tree = leftLeftRotation(tree);
}
} else { // tree是对应要删除的节点。
// tree的左右孩子都非空
if ((tree.left!=null) && (tree.right!=null)) {
if (height(tree.left) > height(tree.right)) {
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 采用这种方式的好处是: 删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。
AVLTreeNode<T> max = maximum(tree.left);
tree.key = max.key;
tree.left = remove(tree.left, max);
} else {
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是: 删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。
AVLTreeNode<T> min = maximum(tree.right);
tree.key = min.key;
tree.right = remove(tree.right, min);
}
} else {
AVLTreeNode<T> tmp = tree;
tree = (tree.left!=null) ? tree.left : tree.right;
tmp = null;
}
}
return tree;
}
public void remove(T key) {
AVLTreeNode<T> z;
if ((z = search(mRoot, key)) != null)
mRoot = remove(mRoot, z);
}
AVL树测试
新建AVL树
依次添加"3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9" 到AVL树中。
2.01 添加3,2 添加3,2都不会破坏AVL树的平衡性。
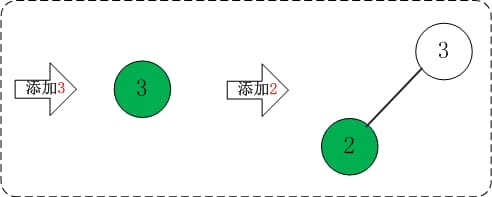
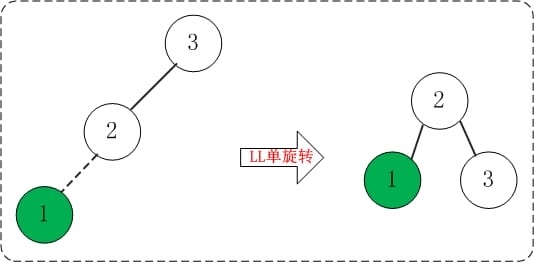
2.02 添加1 添加1之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:
2.03 添加4 添加4不会破坏AVL树的平衡性。
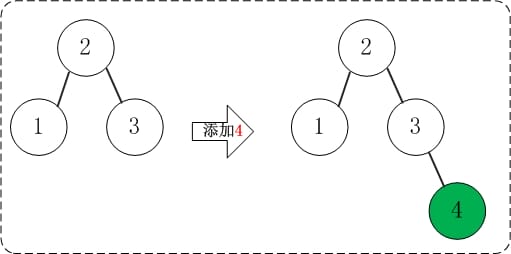
2.04 添加5 添加5之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:

2.05 添加6 添加6之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:

2.06 添加7 添加7之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:

2.07 添加16 添加16不会破坏AVL树的平衡性。

2.08 添加15 添加15之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下:

2.09 添加14 添加14之后,AVL树失去平衡(RL),此时需要对AVL树进行旋转(RL旋转)。旋转过程如下:

2.10 添加13 添加13之后,AVL树失去平衡(RR),此时需要对AVL树进行旋转(RR旋转)。旋转过程如下

2.11 添加12 添加12之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:

2.12 添加11 添加11之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:

2.13 添加10 添加10之后,AVL树失去平衡(LL),此时需要对AVL树进行旋转(LL旋转)。旋转过程如下:

2.14 添加8 添加8不会破坏AVL树的平衡性。

2.15 添加9 但是添加9之后,AVL树失去平衡(LR),此时需要对AVL树进行旋转(LR旋转)。旋转过程如下:

- 打印树的信息
输出下面树的信息:

前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16
中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7
高度: 5
最小值: 1
最大值: 16
- 删除节点8
删除操作并不会造成AVL树的不平衡。

删除节点8之后,再打印该AVL树的信息。
高度: 5
中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16
完整实现和测试的代码
AVL 完整实现代码
/** * Java 语言: AVL树 * * @author skywang * @date 2013/11/07 */
public class AVLTree<T extends Comparable<T>> {
private AVLTreeNode<T> mRoot; // 根结点
// AVL树的节点(内部类)
class AVLTreeNode<T extends Comparable<T>> {
T key; // 关键字(键值)
int height; // 高度
AVLTreeNode<T> left; // 左孩子
AVLTreeNode<T> right; // 右孩子
public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) {
this.key = key;
this.left = left;
this.right = right;
this.height = 0;
}
}
// 构造函数
public AVLTree() {
mRoot = null;
}
/* * 获取树的高度 */
private int height(AVLTreeNode<T> tree) {
if (tree != null)
return tree.height;
return 0;
}
public int height() {
return height(mRoot);
}
/* * 比较两个值的大小 */
private int max(int a, int b) {
return a>b ? a : b;
}
/* * 前序遍历"AVL树" */
private void preOrder(AVLTreeNode<T> tree) {
if(tree != null) {
System.out.print(tree.key+" ");
preOrder(tree.left);
preOrder(tree.right);
}
}
public void preOrder() {
preOrder(mRoot);
}
/* * 中序遍历"AVL树" */
private void inOrder(AVLTreeNode<T> tree) {
if(tree != null)
{
inOrder(tree.left);
System.out.print(tree.key+" ");
inOrder(tree.right);
}
}
public void inOrder() {
inOrder(mRoot);
}
/* * 后序遍历"AVL树" */
private void postOrder(AVLTreeNode<T> tree) {
if(tree != null) {
postOrder(tree.left);
postOrder(tree.right);
System.out.print(tree.key+" ");
}
}
public void postOrder() {
postOrder(mRoot);
}
/* * (递归实现)查找"AVL树x"中键值为key的节点 */
private AVLTreeNode<T> search(AVLTreeNode<T> x, T key) {
if (x==null)
return x;
int cmp = key.compareTo(x.key);
if (cmp < 0)
return search(x.left, key);
else if (cmp > 0)
return search(x.right, key);
else
return x;
}
public AVLTreeNode<T> search(T key) {
return search(mRoot, key);
}
/* * (非递归实现)查找"AVL树x"中键值为key的节点 */
private AVLTreeNode<T> iterativeSearch(AVLTreeNode<T> x, T key) {
while (x!=null) {
int cmp = key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else if (cmp > 0)
x = x.right;
else
return x;
}
return x;
}
public AVLTreeNode<T> iterativeSearch(T key) {
return iterativeSearch(mRoot, key);
}
/* * 查找最小结点: 返回tree为根结点的AVL树的最小结点。 */
private AVLTreeNode<T> minimum(AVLTreeNode<T> tree) {
if (tree == null)
return null;
while(tree.left != null)
tree = tree.left;
return tree;
}
public T minimum() {
AVLTreeNode<T> p = minimum(mRoot);
if (p != null)
return p.key;
return null;
}
/* * 查找最大结点: 返回tree为根结点的AVL树的最大结点。 */
private AVLTreeNode<T> maximum(AVLTreeNode<T> tree) {
if (tree == null)
return null;
while(tree.right != null)
tree = tree.right;
return tree;
}
public T maximum() {
AVLTreeNode<T> p = maximum(mRoot);
if (p != null)
return p.key;
return null;
}
/* * LL: 左左对应的情况(左单旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) {
AVLTreeNode<T> k1;
k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height = max( height(k2.left), height(k2.right)) + 1;
k1.height = max( height(k1.left), k2.height) + 1;
return k1;
}
/* * RR: 右右对应的情况(右单旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) {
AVLTreeNode<T> k2;
k2 = k1.right;
k1.right = k2.left;
k2.left = k1;
k1.height = max( height(k1.left), height(k1.right)) + 1;
k2.height = max( height(k2.right), k1.height) + 1;
return k2;
}
/* * LR: 左右对应的情况(左双旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) {
k3.left = rightRightRotation(k3.left);
return leftLeftRotation(k3);
}
/* * RL: 右左对应的情况(右双旋转)。 * * 返回值: 旋转后的根节点 */
private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) {
k1.right = leftLeftRotation(k1.right);
return rightRightRotation(k1);
}
/* * 将结点插入到AVL树中,并返回根节点 * * 参数说明: * tree AVL树的根结点 * key 插入的结点的键值 * 返回值: * 根节点 */
private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) {
if (tree == null) {
// 新建节点
tree = new AVLTreeNode<T>(key, null, null);
if (tree==null) {
System.out.println("ERROR: create avltree node failed!");
return null;
}
} else {
int cmp = key.compareTo(tree.key);
if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况
tree.left = insert(tree.left, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) == 2) {
if (key.compareTo(tree.left.key) < 0)
tree = leftLeftRotation(tree);
else
tree = leftRightRotation(tree);
}
} else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况
tree.right = insert(tree.right, key);
// 插入节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.right) - height(tree.left) == 2) {
if (key.compareTo(tree.right.key) > 0)
tree = rightRightRotation(tree);
else
tree = rightLeftRotation(tree);
}
} else { // cmp==0
System.out.println("添加失败: 不允许添加相同的节点!");
}
}
tree.height = max( height(tree.left), height(tree.right)) + 1;
return tree;
}
public void insert(T key) {
mRoot = insert(mRoot, key);
}
/* * 删除结点(z),返回根节点 * * 参数说明: * tree AVL树的根结点 * z 待删除的结点 * 返回值: * 根节点 */
private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) {
// 根为空 或者 没有要删除的节点,直接返回null。
if (tree==null || z==null)
return null;
int cmp = z.key.compareTo(tree.key);
if (cmp < 0) { // 待删除的节点在"tree的左子树"中
tree.left = remove(tree.left, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.right) - height(tree.left) == 2) {
AVLTreeNode<T> r = tree.right;
if (height(r.left) > height(r.right))
tree = rightLeftRotation(tree);
else
tree = rightRightRotation(tree);
}
} else if (cmp > 0) { // 待删除的节点在"tree的右子树"中
tree.right = remove(tree.right, z);
// 删除节点后,若AVL树失去平衡,则进行相应的调节。
if (height(tree.left) - height(tree.right) == 2) {
AVLTreeNode<T> l = tree.left;
if (height(l.right) > height(l.left))
tree = leftRightRotation(tree);
else
tree = leftLeftRotation(tree);
}
} else { // tree是对应要删除的节点。
// tree的左右孩子都非空
if ((tree.left!=null) && (tree.right!=null)) {
if (height(tree.left) > height(tree.right)) {
// 如果tree的左子树比右子树高;
// 则(01)找出tree的左子树中的最大节点
// (02)将该最大节点的值赋值给tree。
// (03)删除该最大节点。
// 这类似于用"tree的左子树中最大节点"做"tree"的替身;
// 采用这种方式的好处是: 删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。
AVLTreeNode<T> max = maximum(tree.left);
tree.key = max.key;
tree.left = remove(tree.left, max);
} else {
// 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1)
// 则(01)找出tree的右子树中的最小节点
// (02)将该最小节点的值赋值给tree。
// (03)删除该最小节点。
// 这类似于用"tree的右子树中最小节点"做"tree"的替身;
// 采用这种方式的好处是: 删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。
AVLTreeNode<T> min = minimum(tree.right);
tree.key = min.key;
tree.right = remove(tree.right, min);
}
} else {
AVLTreeNode<T> tmp = tree;
tree = (tree.left!=null) ? tree.left : tree.right;
tmp = null;
}
}
tree.height = max(height(tree.left), height(tree.right)) + 1;
return tree;
}
public void remove(T key) {
AVLTreeNode<T> z;
if ((z = search(mRoot, key)) != null)
mRoot = remove(mRoot, z);
}
/* * 销毁AVL树 */
private void destroy(AVLTreeNode<T> tree) {
if (tree==null)
return ;
if (tree.left != null)
destroy(tree.left);
if (tree.right != null)
destroy(tree.right);
tree = null;
}
public void destroy() {
destroy(mRoot);
}
/* * 打印"二叉查找树" * * key -- 节点的键值 * direction -- 0,表示该节点是根节点; * -1,表示该节点是它的父结点的左孩子; * 1,表示该节点是它的父结点的右孩子。 */
private void print(AVLTreeNode<T> tree, T key, int direction) {
if(tree != null) {
if(direction==0) // tree是根节点
System.out.printf("%2d is root\n", tree.key, key);
else // tree是分支节点
System.out.printf("%2d is %2d's %6s child\n", tree.key, key, direction==1?"right" : "left");
print(tree.left, tree.key, -1);
print(tree.right,tree.key, 1);
}
}
public void print() {
if (mRoot != null)
print(mRoot, mRoot.key, 0);
}
}
AVL 完整测试代码
/** * Java 语言: AVL树 * * @author skywang * @date 2013/11/07 */
public class AVLTreeTest {
private static int arr[]= {3,2,1,4,5,6,7,16,15,14,13,12,11,10,8,9};
public static void main(String[] args) {
int i;
AVLTree<Integer> tree = new AVLTree<Integer>();
System.out.printf("== 依次添加: ");
for(i=0; i<arr.length; i++) {
System.out.printf("%d ", arr[i]);
tree.insert(arr[i]);
}
System.out.printf("\n== 前序遍历: ");
tree.preOrder();
System.out.printf("\n== 中序遍历: ");
tree.inOrder();
System.out.printf("\n== 后序遍历: ");
tree.postOrder();
System.out.printf("\n");
System.out.printf("== 高度: %d\n", tree.height());
System.out.printf("== 最小值: %d\n", tree.minimum());
System.out.printf("== 最大值: %d\n", tree.maximum());
System.out.printf("== 树的详细信息: \n");
tree.print();
i = 8;
System.out.printf("\n== 删除根节点: %d", i);
tree.remove(i);
System.out.printf("\n== 高度: %d", tree.height());
System.out.printf("\n== 中序遍历: ");
tree.inOrder();
System.out.printf("\n== 树的详细信息: \n");
tree.print();
// 销毁二叉树
tree.destroy();
}
}
测试结果
== 依次添加: 3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9
== 前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16
== 中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
== 后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7
== 高度: 5
== 最小值: 1
== 最大值: 16
== 树的详细信息:
7 is root
4 is 7's left child 2 is 4's left child
1 is 2's left child 3 is 2's right child
6 is 4's right child 5 is 6's left child
13 is 7's right child 11 is 13's left child
9 is 11's left child 8 is 9's left child
10 is 9's right child 12 is 11's right child
15 is 13's right child 14 is 15's left child
16 is 15's right child == 删除根节点: 8 == 高度: 5 == 中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 == 树的详细信息: 7 is root 4 is 7's left child
2 is 4's left child 1 is 2's left child
3 is 2's right child 6 is 4's right child
5 is 6's left child 13 is 7's right child
11 is 13's left child 9 is 11's left child
10 is 9's right child 12 is 11's right child
15 is 13's right child 14 is 15's left child
16 is 15's right child
参考文章
本文主要来源于@skywang12345的https://www.cnblogs.com/skywang12345/p/3577479.html,在此基础上重新组织和增加了内容。
其它参考
https://blog.csdn.net/m0_37609579/article/details/99690222